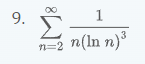
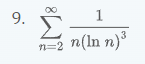
This question has been critiqued by the TA.

Key Points:

if it is in the form of \(u\), you should have different integral points or else use integral of the what you had earlier.
don’t skip steps since there is a step that’s been missed in the form of \((\frac{}{\ln x})\)
say that it is less than \(\infty\)

We use the Integral Test here which is:

If \(\int_2^\infty f(x) \, dx\) convergent, then \(\sum_{n=2}^{\infty} a_n\) is convergent.
If \(\int_2^\infty f(x) \, dx\) convergent, then \(\sum_{n=2}^{\infty} a_n\) is divergent.

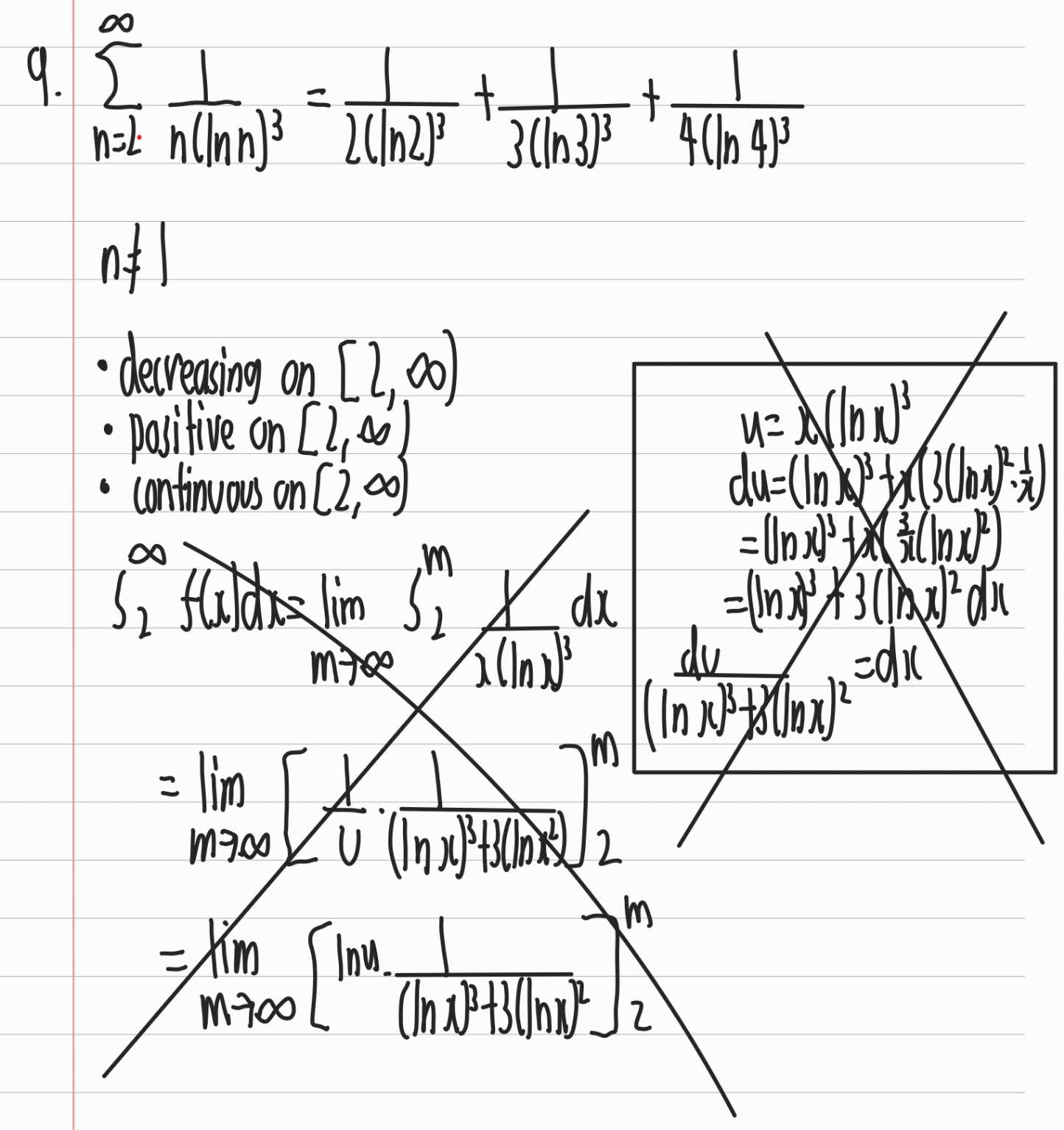
Then you basically take the \(\lim_{m \to \infty} \int_2^m f(x) \, dx\) which in this case is \(\frac{1}{x(\ln x)^3}\).

You proceed to take the integral with U-Substitution and then finally taking the limit.

Since the limit exists, it converges which is the final answer.